问题描述

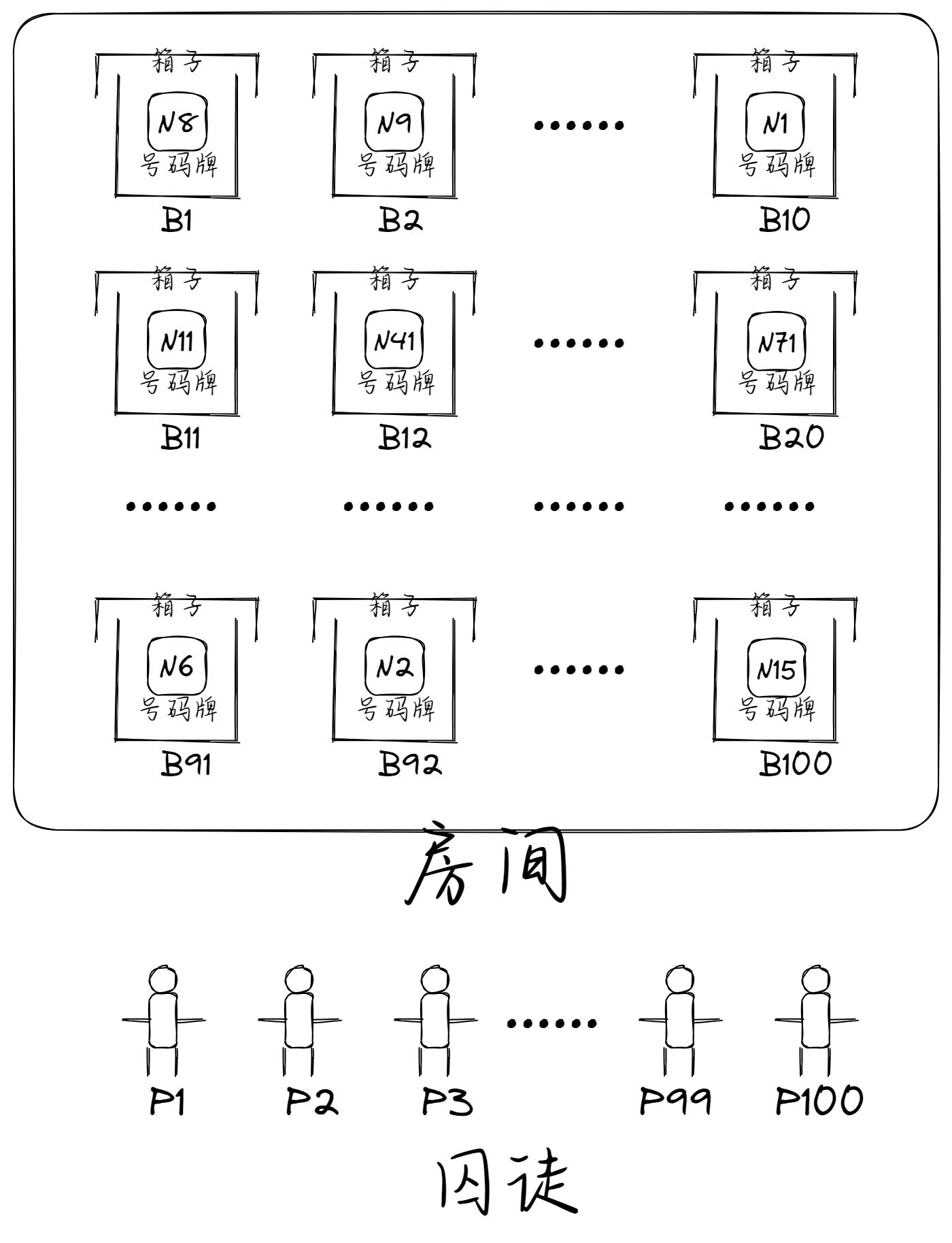
监狱中有 100 名囚犯，编号为 P1-P100。

在房间中有一个橱柜，共有 100 个抽屉，编号为B1-B100。

现有 100 张号码牌，编号为 N1-N100，随机放入 100 个抽屉中（1个抽屉有且仅有1张号码牌）。

现在典狱长决定给囚犯们一次特赦的机会，条件是通过一项挑战。该挑战规则为：

（1）每名囚犯按编号 P1-P100 依次单独进入该房间，自主选择 50 个抽屉打开，并检查抽屉中的号码牌，试图找到与自己编号数字对应的号码牌（如囚犯P6与号码牌N6对应）。囚犯离开房间时，关上所有打开的抽屉，使橱柜恢复原样。

（2）所有囚犯共生共死。如果最终每个囚犯都能找到与自己编号数字对应的号码牌，则挑战成功；存在任何一名囚犯没能找到与自己编号数字对应的号码牌，则挑战失败。

（3）挑战开始前，囚犯可以开会商讨并制定所有人打开抽屉的策略，但挑战开始后，囚犯间不允许进行任何沟通交流。

使用什么样的策略可以最大可能的让囚徒们通过该挑战？最大概率为多少？

问题分析

首先将该挑战整体分割为若干个小挑战，即若囚徒在打开抽屉的过程中找到了与自己编号数字对应的号码牌，则视为该囚徒挑战成功，若所有囚徒都挑战成功，则整个挑战成功。

所以制定的策略，应尽可能的提高不同囚徒挑战结果的相关性，来提高囚徒团队整体的成功率。

最理想的策略是如果囚徒P1成功，那么其他所有囚徒也同样会成功（即相关性），此时囚徒团队整体成功的概率为1/2（实际上无法实现）。

因此需要试着找到一个“使P1与部分囚徒成功率相同”的策略，并验证在该策略下囚徒团队整体的成功率。

问题解答

【策略】对于囚徒 Px，进入房间后，寻找并打开抽屉 Bx（其内的号码牌为 Ny ），接着打开抽屉 By（其内的号码牌为 Nz ），接着打开抽屉 Bz（其内的号码牌为 Nw ），......，按此规律，直至找到与自己编号数字对应的号码牌（挑战成功），或打开完 50 个抽屉（挑战失败）。

【成功率】大于 30%。

问题解析

首先缩小问题规模，简化问题复杂度，便于发现问题解决规律。

假设共 10 名囚徒，每人选择 5 个抽屉打开。

按照上述策略：假设囚徒 P1，打开抽屉 B1（其内号码牌为 N6 ），接着打开抽屉 B6（其内号码牌为 N4 ），接着打开抽屉 B4（期内号码牌为 N1 ），挑战成功。

上述操作，囚徒 P1 依次打开了抽屉 B1，B6，B4，最终挑战成功，我们称为一个闭环（1，6，4），闭环中包含了 m 个数字，则称该闭环长度为 m。很显然：

（1）只有 m<=5 时囚徒才能成功（因为最多开5个抽屉）。

（2）闭环内所有编号对应的囚徒，同时成功或失败，且都将在打开第 m 个抽屉时找到自己对应的号码牌。如对于囚徒P6的闭环为（6，4，1），对于囚徒P4的闭环为（4，1，6）。即闭环内所有编号对应的囚徒成功率相同。

由上分析可知：由于打开抽屉的策略已经确定，因此号码牌的放置顺序决定了团队挑战的成功率。

此时主要考虑以下两点：

（1）共有10个抽屉，依次向每个抽屉放入号码牌，一共有 10！种放法（即 种排列）。

（2）在（1）中的所有排列中，每种排列都可分解为若干个闭环的组合。如排列 {1，6，4，5，2，3，7，9，10，8} 可分解为 闭环（1，6，4）+ 闭环（5）+ 闭环（2，3，7，9，10，8）。

综合以上分析可知，此时问题转换为：团队挑战成功率 = 所有排列分解为闭环后，每个闭环长度都 <=5 的概率。

我们已经找到了该问题中隐藏的数学模型，因此接下来考虑一般情况：

假设共有 2n 个囚犯（即 2n 个抽屉、2n 个号码牌），每个囚犯能打开 n 个抽屉。

号码牌的排列顺序决定了团队挑战的成功率。

假设号码牌的任一种排列，可分解为 k 个闭环 S_1, S_2, ..., S_k，每个闭环的长度分别为 L_1, L_2, ..., L_k，则有：

团队挑战成功率 = 任一闭环 S_i的长度 L_i <= n的概率，即：

其中， P(L_i=l)表示存在长度为 l的闭环的概率。

对于闭环 s，其长度为 l({n+1} \leq {l} \leq {2n})，易知：

（1） 2n个号码牌，共有 2n！种放法（即 A^{2n}_{2n}种排列）

（2）闭环 s中的元素共有 C^{l}_{2n}种选法（即 2n个数中选择 l个作为闭环元素）

（3）选定 l个元素后，这 l个元素可形成 (l-1)！种环排列（即 A^{l-1}_{l-1}种，因为环排列固定首位后，其余元素就等于线排列）

（4）剩下的 2n-l个号码牌，共有 (2n-l)！种放法（即 A^{2n-l}_{2n-l}种排列）

因此：

所以团队挑战成功率：

【回到本问题】

若 2n=100，n=50，则有团队挑战成功率：

【拓展到一般范围】

若 n \rightarrow +\infty，则有团队挑战成功率：

即不管 n 多大，这个策略均可保证 团队挑战成功率 > 30% 。